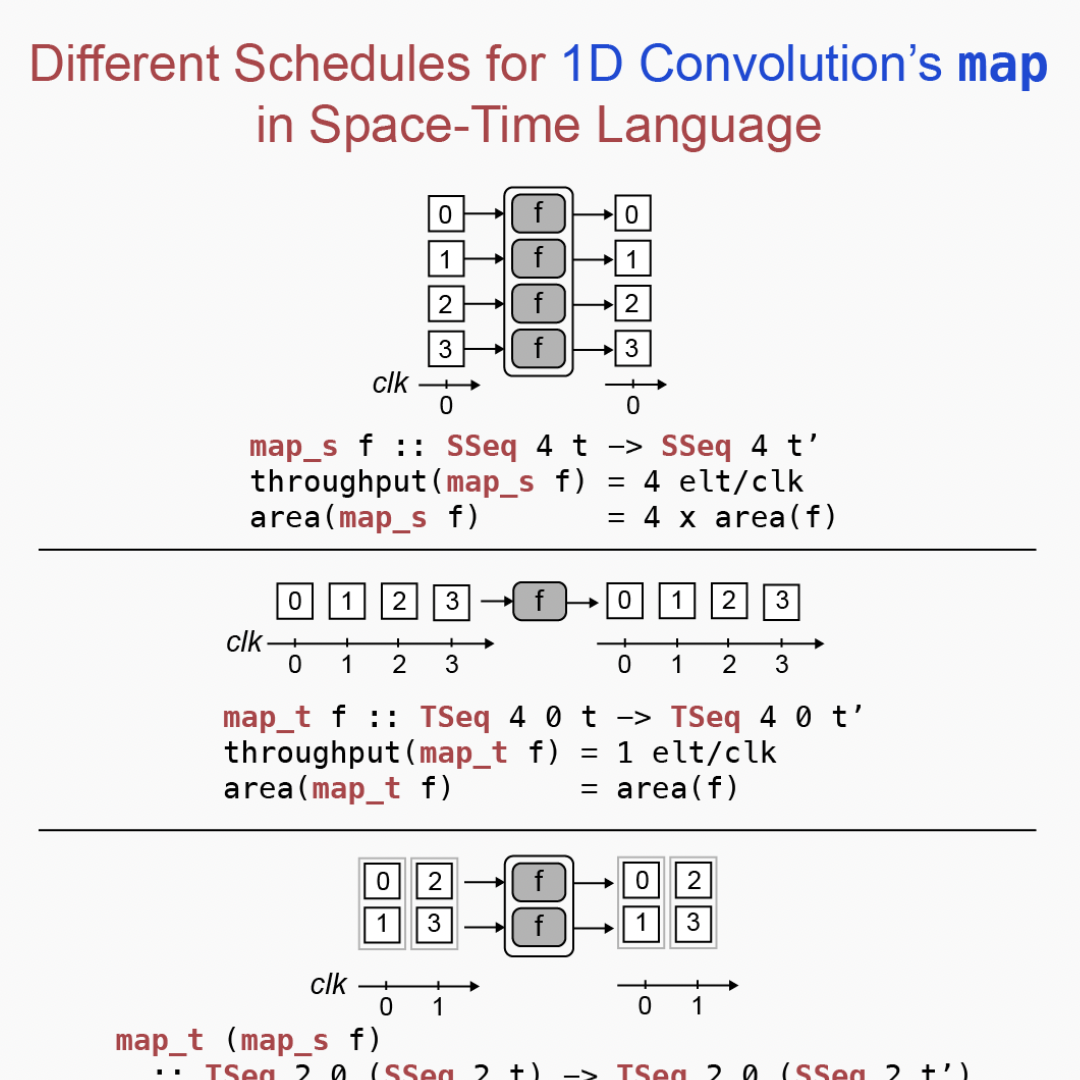
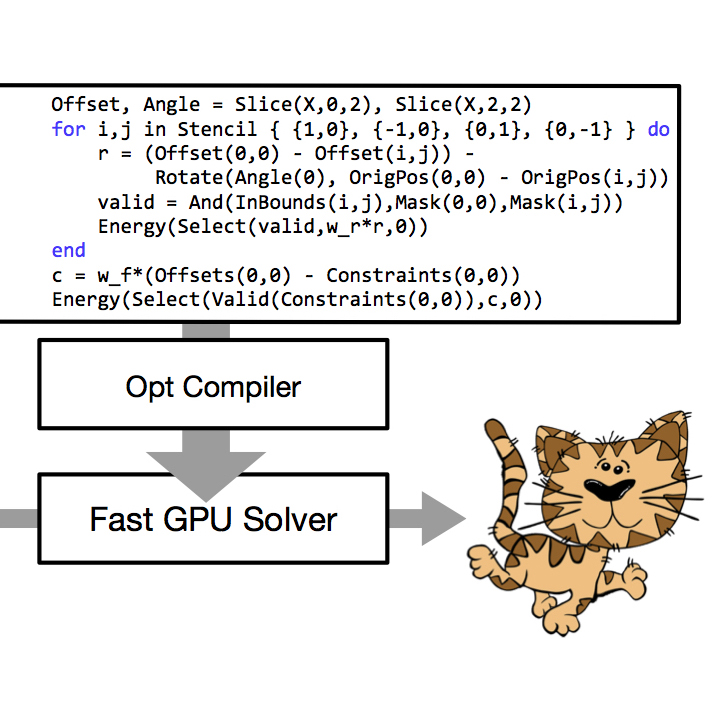
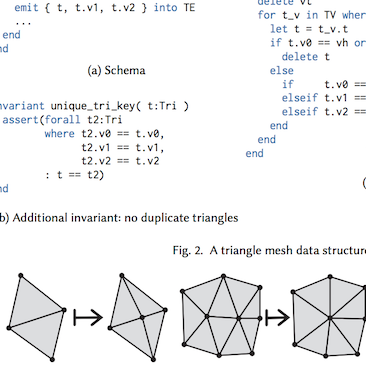
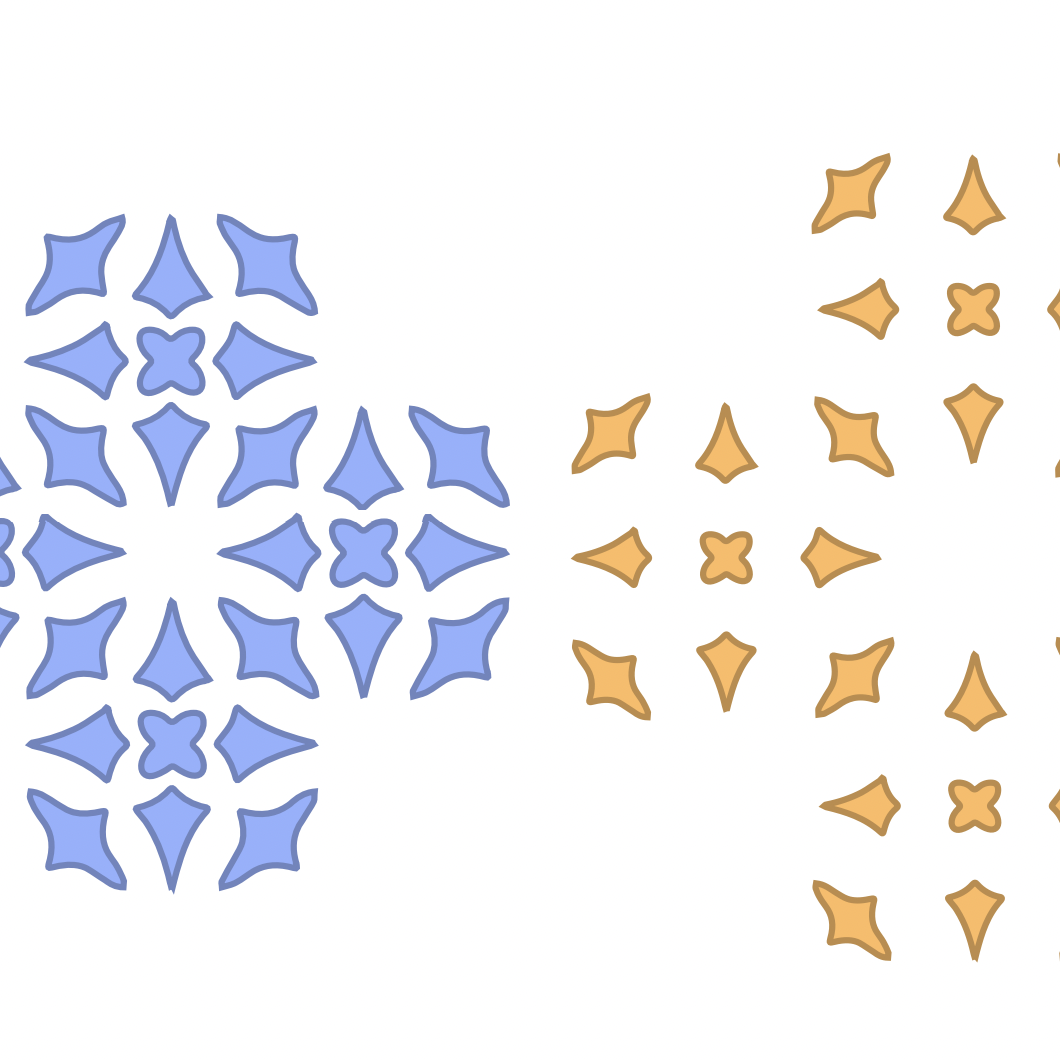
Gilbert Bernstein is a new professor at the University of Washington in Computer Science & Engineering. He specializes in Computer Graphics and Programming Languages, especially high-performance domain-specific languages (DSLs). He was a post-doctorate scholar at UC Berkeley and MIT with Joanthan Ragan-Kelley, and received his PhD from Stanford University working with Pat Hanrahan.
- Debugging CAD Programs (with Felix Hahnlein and Adriana Schulz)
- A Compiler for Finite Element Methods (with Teo Collins and Oded Stein)
- Semantics and Compilation for Knitting Machines (with Jenny Lin, Jim McCann, and others)
- Algebraic Scheduling of Tensor Programs (with Amanda Liu, Jonathan Ragan-Kelley, and Adam Chlipala)
- Exocompilers (with Yuka Ikarashi, Jonathan Ragan-Kelley, and others)
- I am also collaborating on DSLs for networking, Counterstrike bots, gradient-based optimization of chaotic systems, memory management, hardware design languages, and garment design tools.
- Felix Hahnlein (UW Postdoc)
- Ryan Zambrotta (Advising, UW PhD)
- Haoran Peng (Advising, UW PhD)
- Matthew Shang (Advising, UW Undergrad)
- Jiexiao (Jasper) Xu (Advising, UW Undergrad)
- Teo Collins (Mentoring, MIT PhD)
- Amanda Liu (Mentoring, MIT PhD)
- Yuka Ikarashi (Mentoring, MIT PhD)
- David Durst (Mentoring, Stanford PhD)
- Ross Daly (Mentoring, Stanford PhD soon!)
- Alex Reinking (Mentoring, UC Berkeley PhD 2022, now Qualcomm)
- MacKenzie Leake (Mentoring, Stanford PhD 2021, now Adobe Research)
- Differentiable and Probabilistic Programming Langauges (Winter 2024; coming)
- CSE 557: Graduate Computer Graphics (Spring 2023)
an HLSL-like shading language (Slang) with full language support for automatic-differntiation, including generics & interfaces
applying knot theory to the question "what does a program for a knitting machine mean?"
differentiable rendering of implicit surfaces
finding constructible completions of quilting patterns as they're being sketched
a low-level language (and exocompiler) designed to help performance engineers write, optimize, and target high-performance computing kernels onto new hardware accelerators
optimizing imperative array (tensor) code by rewriting functional programs in a verified way using Coq
handling automatic differentiation through discontinuous phenomena, such as collisions, boundaries, and phase changes
A mathematical theory of which quilt designs are constructable via a popular and easy to learn quilting process.
Why are Hardware Design Languages the way they are?
A Domain-Specific Hardware Design Language for trading off transistor usage (space) against pipeline latency (time)
correctness, brevity, and performance for complex geometric data structures
why should we bother designing new programming languages for physical simulation tasks?
a domain-specific language that automatically parallelizes code
exploring design variations while editing geometric patterns by inferring constraints
manipulating apparent objects in icon drawings
fast, efficient boolean library with a C interface
A freeform method for poking holes and merging surfaces
getting characters to turn on a dime, using non-parametric alternatives to motion graphs
robust boolean operations that are fast enough for interactive use.
knot theory meets graph theory. Hunting for the elusive minor minimal intrinsically knotted graphs